Maths
Apex Collaborative Trust follows a curriculum that engineers success using a mastery approach. Reference to the NCETM Spines ensures small step progression through careful curriculum sequencing.
The curriculum is split into declarative, procedural and conditional knowledge which are encompassed within the NCETM’S five Big Ideas; Representation and Structure, Mathematical Thinking, Variation, Fluency and Coherence.
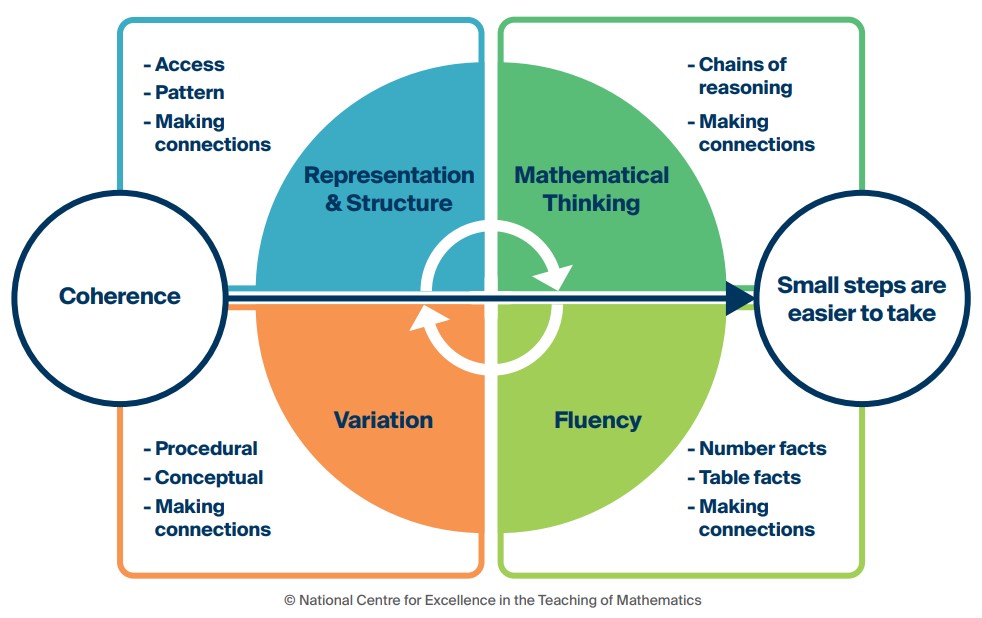
Using guidance and advice from the NCETM, curriculum leads have identified declarative knowledge needed for automaticity. Opportunities to both learn and use this knowledge are given until both speed and accuracy of recall is achieved.
Again, with guidance from the NCETM Spines, procedural knowledge is integrated within our curriculum by teaching efficient and accurate methods of calculations to enabled fluidity in systematic methods, algorithms, or procedures.
Within their learning, children can combine declarative and procedural knowledge, which feeds into mathematical reasoning and problem-solving tasks. This can consist of abstract, real world, routine, or non-routine problems. This is their opportunity to showcase the conditional knowledge.
The NCETM "spine" documents under-pin our pedagogical approach and ensure teachers can plan and deliver lessons that align with the DfE's non-statutory guidance for teaching mathematics whilst meeting the needs of the children in their class. However, we do not merely use the NCETM materials as a scheme. Careful planning and preparation enable teachers to draw on the pedagogical approaches whilst sourcing appropriate, bespoke questions and activities from banks of well-prepared additional resources.
Small steps for both declarative and procedural understanding are planned for, giving due consideration to common misconceptions that are likely to occur. The NCETM ‘Making Connections’ document enables children to make links between previous learning and further challenge is added in the form of questioning or delving deeper into a concept in more detail. In order for children to retrieve knowledge from long-term memory ‘curve ball’ questions and ‘It’s nothing new’ is carefully considered and planned into the curriculum.
Our overall aim is to prevent widened gaps in learning by having coherently planned units, which provide teachers with some autonomy to tailor teaching so that it is adapted to meet the needs and next steps of all learners. The reactive aspect of the curriculum allows teachers to seek out these gaps and implement appropriated measures such as timely interventions or pre learning opportunities.
Teachers have high expectations of all pupils with SEND. Teachers do not compromise the requirement for overlearning to ensure automaticity. Staff will also decide whether to wait, or whether to act approach. This means that there is no automatic assumption that pupils identified as SEN cannot achieve. Early identification of gaps is a key component of our approach. Drawing from the DfE Ready to Progress document, teachers identify and assess gaps in learning within a cohort. Furthermore, diagnostic assessment tools such as Sandwell Early Numeracy Assessment ascertain the next small steps for the very small proportion of pupils progressing outside the age-related expectations of their year group.
EYFS
For continuity and progression of content, EYFS will draw upon the White Rose overview to craft bespoke learning that meets the needs of the children.
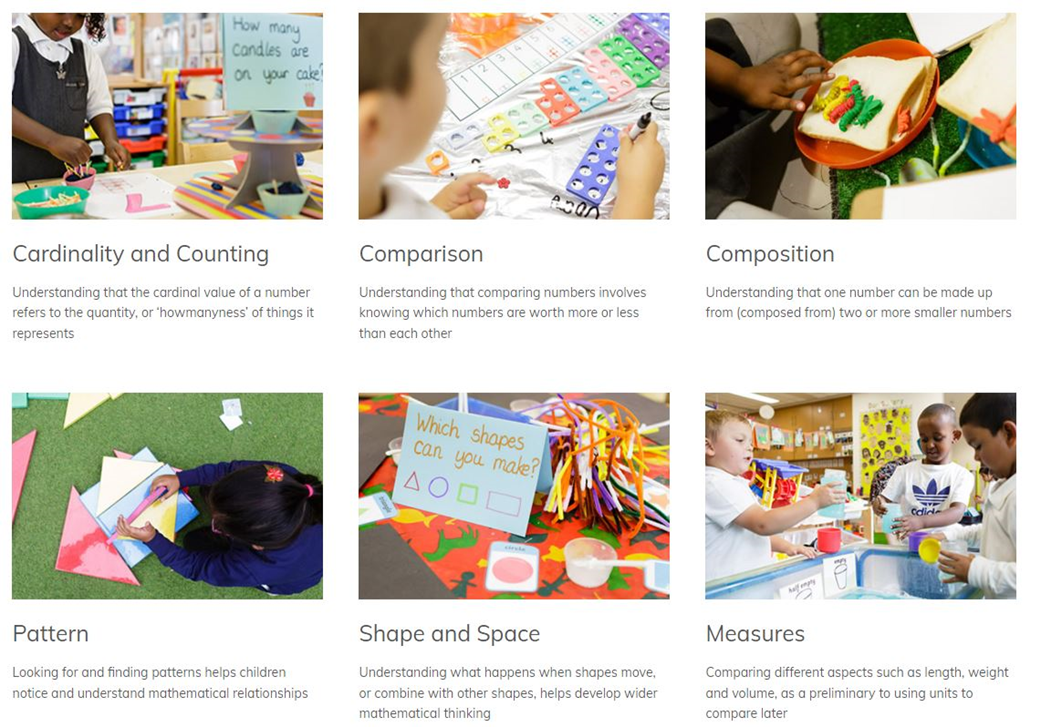
We use the six key areas of early mathematics learning to collectively provide a platform for everything children will encounter as they progress through their maths learning at primary school, and beyond.
Assessment
Fundamental to the effectiveness of our curriculum is our approach to assessment. We utilise a responsive approach to assessment strategies which focus on moving the learning forward and the activation of learners as owners of their own learning. We recognise that effective feedback should be specific, accurate and timely and provide clear guidance on how to improve. Pupils are explicitly taught meta cognitive strategies through dialogic talk as well as how to monitor, plan and evaluate their learning. The information provided by assessments is essential for planning and adaptive teaching.
In addition to this, children also complete end of term assessments and retrieval assessments assessing the previous units of maths.
Quality Assurance
We have developed a collaborative approach to quality assurance which supports teachers to reflect and refine the sequencing of the core knowledge and foundational concepts for their subjects, evaluate the effectiveness of the principles of direct instructional teaching whilst securing the skills to know when knowledge is secure before pupils move on.
The rationale of our mathematics curriculum is based upon guidance from:
The Education Endowment Foundation Improving Mathematics in Early Years, Key Stage 1, Key Stage 2 and 3 Improving Mathematics in the Early Years and Key Stage 1 | EEF (educationendowmentfoundation.org.uk) Improving Mathematics in Key Stages 2 and 3 | EEF (educationendowmentfoundation.org.uk)
The Ofsted Research Review of Mathematics Research review series: mathematics - GOV.UK (www.gov.uk)
The Department for Education ready to progress non statutory guidance Mathematics guidance: key stages 1 and 2 (covers years 1 to 6) (publishing.service.gov.uk)
The National Centre for the Teaching of mathematics (NCETM) Home | NCETM





